Review of Algebraic Subtraction
Algebra Help: Section 2.11
Subtraction is the process of finding the difference between two quantities.
Find the difference between similar terms.
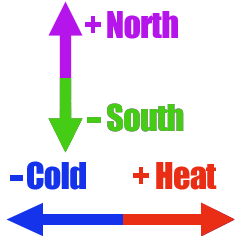
1. A and B travel north
from the same point. The distance A
travels is 7m. The the distance B
travels is 4m. How much father north is A
than B?
OPERATION
Minuend 7m
Subtrahend 4m
____
Algebraic Difference 3m
ANALYSIS - A traveled farther north
than B, as A's distance, 7m
exceeds B's distance, 4m. The answer is 3m.
7m - 4m = 3m.
2. A and B start from the same point. A
travels north a distance of 7m. B
travels south a distance of 4m.
How much farther north is A than B?
OPERATION
Minuend + 7m
Subtrahend - 4m
____
Difference +11m
ANALYSIS - To express the distances
algebraically, indicate different directions
by opposite signs; north by plus,
south by minus.
Since A traveled 7m north,
while B traveled 4m south,
A must be 11m farther north
than B, and to indicate this direction from
B, we must use the +
sign, thus +11m.
The expression 11m, in the last example, is
called the algebraic difference of +
7m and - 4m,
because it denotes the difference apart.
To subtract, in algebra, is not in all cases
to decrease. Consider positive and negative quantities
in opposite circumstances, or counted in opposite directions.
Therefore
the difference, or space between them, is their apparent sum.
If we want the difference in latitude between a place
7 degrees north and a distance 4 degrees south,
the answer is 7 + 4.
This principle is further illustrated by the example below, in which it is plain that the remainders, for positive subtrahends, in the lower line must decrease by 2 throughout. The remainders, for negative subtrahends, in the lower line must increase by 2 throughout. To obtain the true result, the sign of - 2 and - 4 must be changed to +.
3.
From 16 16 16 16 16
Take 4 2 0 -2 -4
___ ___ ___ ___ ___
Remainder 12 14 16 18 20
4. From +7a subtract +
12a.
OPERATION:
Minuend + 7a
Subtrahend + 12a
_____
Difference - 5a
ANALYSIS - We change the sign of the subtrahend
as in other examples; then the sum of - 12a
and + 7a is - 5a,
the algebraic difference.
5. OPERATION
From 15a 10a 5a 0
Take 5a 5a 5a 5a
_____________
Difference, 10a 5a 0 -5a
ANALYSIS - Since the minuends decrease by 5a toward
the right, and the subtrahends are all equal,
the remainders must decrease by 5a,
and the last remainder is therefore -5a.
We cannot, numerically, take a greater quantity from a less, nor any quantity
from zero, for no quantity can be less than nothing.
Hence, in the last two examples, the answer - 5a, is not
5a less than nothing, but 5a applied in the opposite
direction to + 5a. To subtract a quantity algebraically,
is to change the direction in which it is applied.
Thus, we see that by a change of sign, we can find the algebraic difference between any two quantities,
whatever.
From these examples and illustrations we derive the following rule.
RULE - Change the sign of the subtrahend, or conceive it to be changed, and unite the terms as in addition.
Pages 33-35
Pages 33-35
Help with Algebra Homework
Free tutorials provide math help for math problems. Tutorials start with algebra 1. Algebra tutorials include word problems related to algebra topics, as they're introduced. See the menu, above for algebra math equations, and explanation, by section.
Windows algebra games, designed to help with classwork, coming soon!
Windows games, in progress, work with this set of free tutorials, modified
from the public domain text book titled,
New Elementary Algebra
containing the rudiments of the science for schools and academies.
By Horation N Robinison, LL. D. Ivison, Blakeman & Company, Publishers, New York and Chicago.



