Sum Coefficients

Algebra Help: Section 2.3

Learn to sum coefficients.

Steps to Sum Coefficients

A coefficient's described as follows from section 1.2, algebraic Quantities:

A Coefficient is a number or quantity prefixed to another quantity, to denote how many times the latter is taken; thus, in 3x, 3 is the coefficient of x, and indicates that x is taken 3 times. In 3ax, 3 may be regarded as the coefficient of ax, or 3a as the coefficient of x. In 4(a + x), 4 is the coefficient of (a + x). When no coefficient is written, the unit 1 is understood.

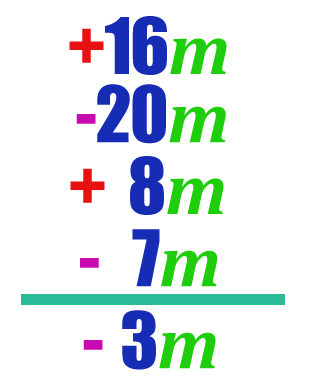
Practice: Sum Coefficients

3. A ship started at the equator and sailed the first day 16 miles north, the second day 20 miles south, the third day 8 miles north, and the fourth day 7 miles south. How far from the equator, and in what latitude, was the ship at the end of four days?

FIRST OPERATION:

+ 16m - 20m
+  8m  - 7m
____________
+ 24m - 27m = -3m

ANALYSIS - We let m represent 1 mile; and to distinguish directions, we indicate distance north by the plus sign, and distance south by the minus sign, writing the positive terms in one column and the negative terms in another column. The whole distance sailed north, is the sum of 16m plus 8m, or 24m. The whole distance sailed south, is the sum of 20m and 7m, or 27m. 27 is 3 more than 24, the ship must be three miles south of the equator, expressed algebraically thus, - 3m.

SECOND OPERATION:

+ 16m
- 20m
+  8m
-  7m
_______
-  3m

ANALYSIS - In the second operation we write all the terms in one column, since they are similar. The sum of +16m and +8m is +24m. The sum of -20m and -7m is -27m. +24m - 27m equals -3m, the algebraic sum of the quantities in the column.

NOTE - There is a distinction between arithmetic and algebraic addition. In the above example, had the question been, how far the ship sailed, the answer would be 16 + 20 + 8 + 7 = 51 miles, or 51m, which is the arithmetical sum of the distances sailed. But the real question is, What distance, north or south, did the ship make from the starting point?. The answer is 3 miles south, or -3m, which is the algebraic sum of the distances sailed. Adding, in algebra, does not always increase values. Positive and negative quantities represent things opposite in kind or quality, and if similar in denomination, are added or united, by apparent subtraction.

From these examples and illustrations we derive the following rules.

RULES:

In the same manner similar quantities, of whatever kind, may be added by taking the algebraic sum of their coefficients. Notice that, since 2 times any number whatever, added to three times the same number, are 5 times that number, so the sum of 2(a + b) and 3(a + b) is 5(a + b).

26-27

26-27

Help with Algebra Homework

Free tutorials provide math help for math problems. Tutorials start with algebra 1. Algebra tutorials include word problems related to algebra topics, as they're introduced. See the menu, above for algebra math equations, and explanation, by section.

Windows algebra games, designed to help with classwork, coming soon! Windows games, in progress, work with this set of free tutorials, modified from the public domain text book titled, New Elementary Algebra containing the rudiments of the science for schools and academies. By Horation N Robinison, LL. D. Ivison, Blakeman & Company, Publishers, New York and Chicago.

Tags