Help Solve for One Angle
Level 4
Trig Triumph Game Trigonometry Help
Win 40 points for each correct selection. This page explains how to solve for one angle of a right triangle.
Calculator for Degrees, Minutes, and Seconds
Questions in the Trig Triumph
game include angles with degrees, minutes and seconds.
The calculator allows you to insert degree, minute, and second
symbols. However the calculator doesn't execute statements
with degrees, minutes, or seconds. This section
teaches you how to solve for one angle, with degrees, minutes, and seconds.
Before submitting your final answer, always include the degree symbol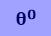 
.
If the angle breaks down to minutes and seconds
include the minute symbol 
and the second symbol 
.
Use the calculator button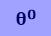
to insert the degree symbol .
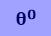Use the calculator button
to insert the minute symbol .
Use the calculator button
to insert the second symbol .
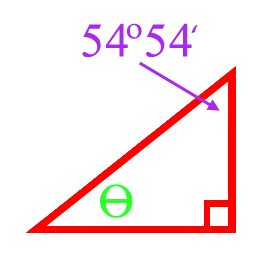
Solve for Angles in Degrees
The sum of all three angles in a triangle equals 1800 or 180 degrees. A right angle equals 90 degrees. In a right triangle, the sum of the two remaining angles equals 90 degrees because 180 - 90 = 90. Each question includes a right angle, and the value for a second angle θ.
The formula:
180 = 90 (the right angle) + θ (The given angle) + θ.
Solve for the remaining angle θ.
For example given θ = 60. Substitute θ for 60 in the previous formula.
180 = 90 + 60 + θ 180 - 90 = 60 + θ 90 = 60 + θ 90 - 60 = θ 30 = θ
The remaining angle solution is 30.
Solve for Angles with Degrees, Minutes, and Seconds
Minutes
Each degree may be divided into 60 minutes. One minute equals 1/60 of a degree. One degree equals 60 minutes. The symbol for degree is 0. The symbol for minute is '.
Seconds
Each minute may be divided into 60 seconds. One second equals 1/60 of a second. One minute equals 60 seconds. The symbol for seconds is ''.
One degree equals 3600 seconds because 60 minutes times 60 seconds equals 3600.
Use a modification of the previous formula to solve for angle θ given θ = 6002'.
1800 = 900 + 6002' + θ. 1800 - 900 = 6002' + θ. 900 - 6002' = θ.
Subtract 6002' from 9000'.
9000'
-6002'
Borrow one degree from 900 to add 60 minutes. Remember 89060' = 9000'. Now subtract 89060' - 6002' = θ.
89060'
-600 2'
_________________________
29058'
Your solution is 29058' = θ.
Follow the same process with seconds. Borrow 60 seconds from the minutes column when necessary.
Scoring
Each correct answer equals 40 points. Level 4 includes 10 questions. The maximum score for level 4 equals 400 points.
Post Your Score Online
Select the Post Score
button to post your score online.
See how your score compares to others in the Trig Triumph Hall of Fame.
Rounding Errors
Trig Triumph rounds the final answer to the nearest thousandth (3 digits after the decimal point). Often rounding each step in a series introduces rounding errors. The final result may be too high, when more than one step in the series rounds up. The final result may be too low, when more than one step in the series rounds down.
Therefore don't round each step. Round the final answer down to the nearest thousandth. The Trig Triumph game allows for small rounding differences. However it's helpful to understand for future math projects.
Reset Level Four
Select the Reset
button at the bottom of the page, to
begin this level again. Reset
allows you to play the
level over again and increase your score. Reset
assigns zero to
your score for this level, then displays the first question for this level.
Trigonometry Help
Read short trigonometry tutorials.
Each tutorial also leads to a level of the Trig Triumph
game.
Play the game level to learn the section while
also having a little fun.
Trigonometry helps programmers, engineers, scientists, teachers, and students. Trigonometry provides a foundation with mathematics required for game programming, science, technology, engineering, and math (STEM).
Love learning trigonometry with tutorials, games and graphics!
